(Note: This post is copied verbatim from this MSE question.)
Let $N = q^k n^2$ be an odd perfect number with special prime $q$ satisfying $q \equiv k \equiv 1 \pmod 4$ and $\gcd(q,n)=1$.
Define the abundancy index
$$I(x)=\frac{\sigma(x)}{x}$$
where $\sigma(x)$ is the classical sum of divisors of $x$.
Since $q$ is prime, we have the bounds
$$\frac{q+1}{q} \leq I(q^k) < \frac{q}{q-1},$$
which implies, since $N$ is perfect, that
$$\frac{2(q-1)}{q} < I(n^2) = \frac{2}{I(q^k)} \leq \frac{2q}{q+1}.$$
By considering the negative product
$$\bigg(I(q^k) - \frac{2(q-1)}{q}\bigg)\bigg(I(n^2) - \frac{2(q-1)}{q}\bigg) < 0,$$
since we obviously have
$$\frac{q}{q-1} < \frac{2(q-1)}{q},$$
then after some routine algebraic manipulations, we arrive at the lower bound
$$I(q^k) + I(n^2) > 3 - \frac{q-2}{q(q-1)} = \frac{3q^2 - 4q + 2}{q(q - 1)}.$$
Now, a recent MO post improves on the lower bound for $I(n^2)$, as follows:
$$I(n^2) > \bigg(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\bigg)$$
Repeating the same procedure as above, we have the negative product
$$\Bigg(I(q^k) - \left(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\right)\Bigg)\Bigg(I(n^2) - \left(\frac{2(q-1)}{q}\bigg)\bigg(\frac{q^{k+1} + 1}{q^{k+1}}\right)\Bigg) < 0.$$
This implies, after some algebraic manipulations, that
$$I(q^k) + I(n^2) > \frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}}.$$
But WolframAlpha says that the partial fraction decomposition of the new lower bound is given by
$$\frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}} = \frac{3q^2 - 4q + 2}{q(q - 1)} + \frac{2(q - 1)}{q^{k+2}} - \frac{q}{(q - 1)(q^{k+1} + 1)}.$$
So essentially, my question boils down to:
QUESTION: Is it possible to produce an unconditional proof (that is, for all $k \geq 1$ and for all special primes $q \geq 5$) for the following inequality?
$$\frac{2(q - 1)}{q^{k+2}} > \frac{q}{(q - 1)(q^{k+1} + 1)}$$
MY ATTEMPT
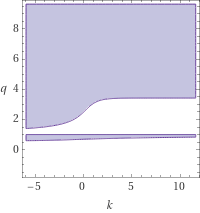
I tried to ask WolframAlpha for a plot of the above inequality, it gave me the following GIF image:
WolframAlpha Inequality Plot
So it does appear that the inequality is unconditionally true, which would mean that the new lower bound for $I(q^k) + I(n^2)$ improves on the old. Is it possible to prove this analytically?
And lastly: Based on this answer to a closely related question, since we appear to have obtained an improved lower bound for $I(q^k) + I(n^2)$, can we then say that there is indeed an integer $a$ such that $k \leq a$?
Posted Answer
Suppose to the contrary that there exists an integer $k \geq 1$ and a (special) prime $q \geq 5$ such that
$$\frac{q}{(q-1)(q^{k+1}+1)} \geq \frac{2(q-1)}{q^{k+2}}.$$
This inequality is equivalent to
$$q^{k+3} \geq 2(q-1)^2 (q^{k+1}+1) = 2q^{k+1} - 4q^{k+2} + 2q^{k+3} + 2q^2 - 4q + 2,$$
which in turn is equivalent to
$$0 \geq q^{k+3} - 4q^{k+2} + 2q^{k+1} + 2q^2 - 4q + 2 = q^{k+2} (q - 4) + 2q^{k+1} + 2q(q - 2) + 2 > 0,$$
a contradiction.
We therefore conclude that
$$\frac{2(q-1)}{q^{k+2}} > \frac{q}{(q-1)(q^{k+1}+1)}$$
for all integers $k \geq 1$ and all (special) primes $q \geq 5$.
Hence, the new lower bound
$$I(q^k) + I(n^2) > \frac{q^{k+2}}{(q - 1)(q^{k+1} + 1)} + \frac{2(q-1)(q^{k+1} + 1)}{q^{k+2}}$$
does indeed improve on the old lower bound
$$I(q^k) + I(n^2) > 3 - \frac{q-2}{q(q - 1)} = \frac{3q^2 - 4q + 2}{q(q - 1)}.$$
It remains to be seen whether this implies that there does exist an integer $a$ such that $k \leq a$, if $q^k n^2$ is an odd perfect number with special prime $q$.